log (latency) = log (tmax + δ)  log (tmax) log (tmax) |
| (1) |
|
|
 S consists of
the sum of latencies of their components:
S consists of
the sum of latencies of their components:
| (2) |
 T it is necessary to solve the system of
linear Equations 2, which is usually impossible because
||T ||
T it is necessary to solve the system of
linear Equations 2, which is usually impossible because
||T || 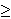 ||S || (there are usually fewer paths than time
components).
Non-linear logarithmic filtering is a common technique used in
physics and economics to select only the major sum
contributors [22]. We used latency filtering to select
the most important latency contributors tmax and filter
out the other latency components δ:
||S || (there are usually fewer paths than time
components).
Non-linear logarithmic filtering is a common technique used in
physics and economics to select only the major sum
contributors [22]. We used latency filtering to select
the most important latency contributors tmax and filter
out the other latency components δ:
|
|
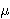 s,
a full stroke disk head seek takes approximately 8ms,
a full disk rotation takes approximately 4ms,
the network latency between our test machines is about 112
s,
a full stroke disk head seek takes approximately 8ms,
a full disk rotation takes approximately 4ms,
the network latency between our test machines is about 112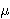 s,
and the scheduling quantum is about 58ms.
Therefore, if some of the profiles have peaks close to these times,
then we can hypothesize right away that they are related to the
corresponding OS activity.
For any test setup, these and many other characteristic times can
be measured in advance by profiling simple workloads that are
known to show peaks corresponding to these times.
It is common that some peaks analyzed for one workload in
one of the OS configurations can be recognized later on new
profiles captured under other circumstances.
Differential profile analysis
While analyzing profiles, one usually makes a hypothesis about a potential
reason for a peak and tries to verify it by capturing a different profile
under different conditions. For example, a lock contention should disappear
if the workload is generated by a single process. The same technique
of comparing profiles captured under modified conditions (including OS code or
configuration changes) can be used if no hypothesis can be made.
However, this usually requires exploring
and comparing more sets of profiles. As we have already described in
this section, we have designed procedures to compare two different
sets of profiles automatically and select only those that differ
substantially. Section 3.2 discusses these profiles,
comparing procedures in more detail.
Layered profiling
s,
and the scheduling quantum is about 58ms.
Therefore, if some of the profiles have peaks close to these times,
then we can hypothesize right away that they are related to the
corresponding OS activity.
For any test setup, these and many other characteristic times can
be measured in advance by profiling simple workloads that are
known to show peaks corresponding to these times.
It is common that some peaks analyzed for one workload in
one of the OS configurations can be recognized later on new
profiles captured under other circumstances.
Differential profile analysis
While analyzing profiles, one usually makes a hypothesis about a potential
reason for a peak and tries to verify it by capturing a different profile
under different conditions. For example, a lock contention should disappear
if the workload is generated by a single process. The same technique
of comparing profiles captured under modified conditions (including OS code or
configuration changes) can be used if no hypothesis can be made.
However, this usually requires exploring
and comparing more sets of profiles. As we have already described in
this section, we have designed procedures to compare two different
sets of profiles automatically and select only those that differ
substantially. Section 3.2 discusses these profiles,
comparing procedures in more detail.
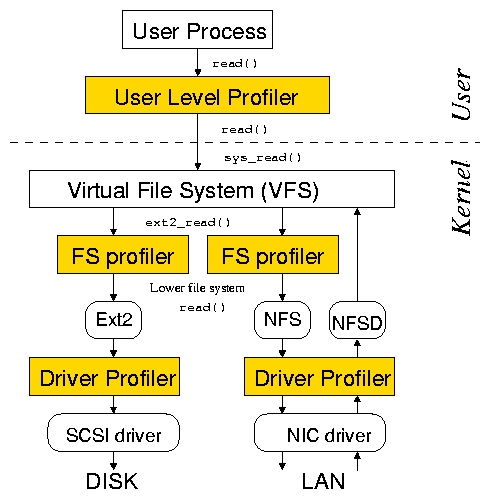
Layered profiling
| (3) |
 20ns). Also, it is
possible to synchronize the counters in software by writing to them
concurrently. For example, Linux synchronizes CPU clock counters at
boot time and achieves timing synchronization of
20ns). Also, it is
possible to synchronize the counters in software by writing to them
concurrently. For example, Linux synchronizes CPU clock counters at
boot time and achieves timing synchronization of 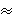 130ns.
Profile Locking Bucket increment operations are not atomic
by default on most CPU architectures. This means that if two threads
attempt to update the same bucket concurrently only one of them will
succeed. A naïve solution would be to use atomic
memory updates (the lock prefix on i386). Unfortunately, this
can seriously affect profiler performance.
Therefore, we adopted two alternative solutions based on the number of CPUs:
(1) If the number of CPUs is small, the probability that two or more
bucket writes happen at the same time is small. Therefore,
the number of missed profile updates is small.
For example, in the worst case scenario for a dual-CPU system, we observed
that less than 1% of bucket updates were lost while two threads
were concurrently measuring latency of an empty function and updating
the same bucket. For real workloads this number is much smaller because
the profiler updates different buckets and the update frequency is smaller.
Therefore, we use no locking on systems with few CPUs.
(2)
The probability of concurrent updates grows rapidly as the number of
CPUs increases.
On systems with many CPUs
we make each process or thread update its own profile in memory.
This prevents lost updates on systems with any number of CPUs.
130ns.
Profile Locking Bucket increment operations are not atomic
by default on most CPU architectures. This means that if two threads
attempt to update the same bucket concurrently only one of them will
succeed. A naïve solution would be to use atomic
memory updates (the lock prefix on i386). Unfortunately, this
can seriously affect profiler performance.
Therefore, we adopted two alternative solutions based on the number of CPUs:
(1) If the number of CPUs is small, the probability that two or more
bucket writes happen at the same time is small. Therefore,
the number of missed profile updates is small.
For example, in the worst case scenario for a dual-CPU system, we observed
that less than 1% of bucket updates were lost while two threads
were concurrently measuring latency of an empty function and updating
the same bucket. For real workloads this number is much smaller because
the profiler updates different buckets and the update frequency is smaller.
Therefore, we use no locking on systems with few CPUs.
(2)
The probability of concurrent updates grows rapidly as the number of
CPUs increases.
On systems with many CPUs
we make each process or thread update its own profile in memory.
This prevents lost updates on systems with any number of CPUs.
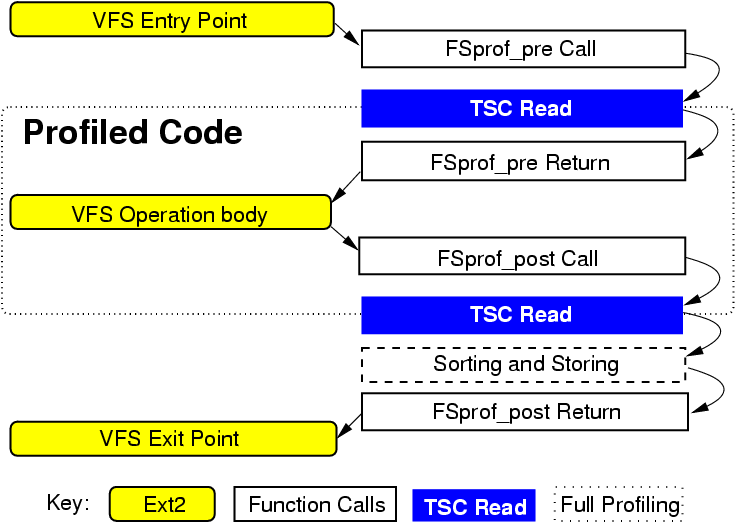
{
f_type tmp_return_variable = foo(x);
FSPROF_POST(op);
return tmp_return_variable;
}
struct file_operations ext2_dir_operations = {
read: generic_read_dir,
readdir: ext2_readdir,
ioctl: ext2_ioctl,
fsync: ext2_sync_file,
};
|
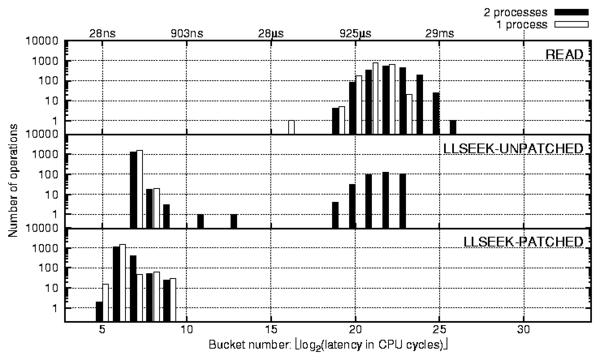
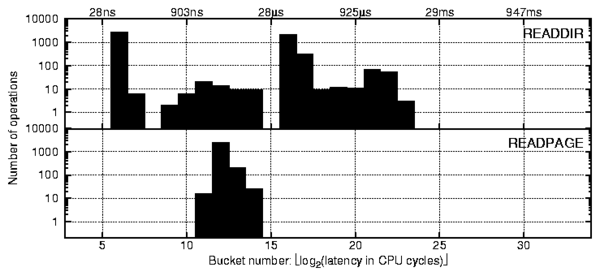
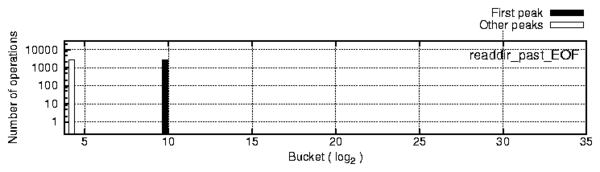
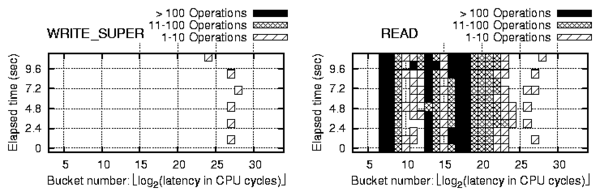
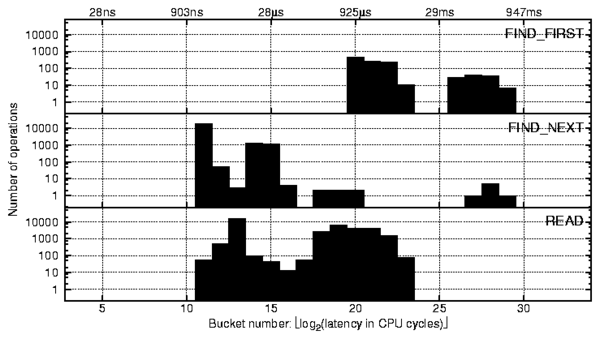
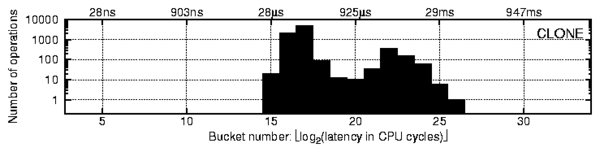
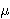 s) involve
interaction with the server,
whereas buckets to the left of it were local to the client. All of
the FindFirst operations here go through the server, as do the
rightmost two peaks of the FindNext operation.
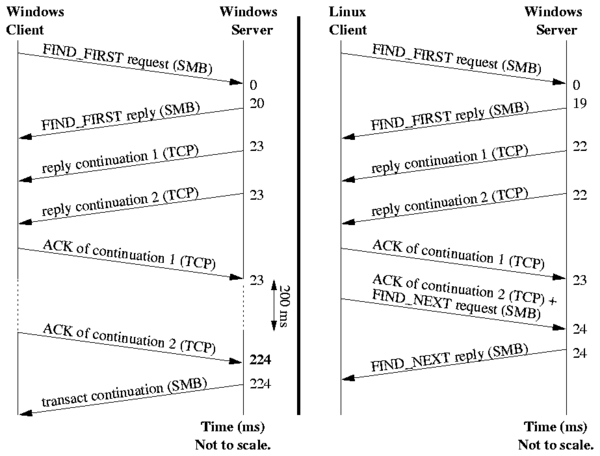
We ran a packet sniffer on the network to investigate this further.
s) involve
interaction with the server,
whereas buckets to the left of it were local to the client. All of
the FindFirst operations here go through the server, as do the
rightmost two peaks of the FindNext operation.
We ran a packet sniffer on the network to investigate this further.